BANGUN RUANG SISI LENGKUNG KELAS IX KURIKULUM 2006 BERIKUT CONTOH SOAL DAN GAMBAR
Daftar Isi
Haii teman-teman, hari ini kita akan mempelajari mengenai Bangun Ruang Sisi Lengkung. Bangun ruang sisi lengkung di bedakan menjadi 3 yaitu: Tabung, Kerucut dan Bola
Nilai π adalah 22/7 atau 3,14
22/7 hanya digunakan jika bilangan bisa dibagi 7 dan jika 3,14 digunakan jika bilangan tidak bisa dibagi 7
Contoh 1 :
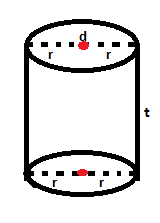
1. Sebuah kaleng berbentuk tabung dengan jari-jari 7cm, tinggi 15cm, dan π 22/7. Hitunglah
a. L. alas
b. L. selimut
c. L. permukaan
d. Volume
Jawab :
a. L. alas = πr² = 22/7 × 7 × 7 = 154 cm²
b. L. selimut = 2πrt = 2 × 22/7 × 7 × 15 = 660 cm²
c. L . permukaan = 2πr² + 2πrt
= (2 × 154) + 660
= 306 + 660 = 968 cm²
d. Volume = L. alas × t
= 154 × 15 = 2310 cm³
Contoh 2 :
2. Sebuah drum dengan diameter 20dm, tinggi 25dm dan π 3,14. Hitunglah
a. L. alas
b. L. selimut
c. L. permukaan
d. Volume
d = 20dm = r = 20 ÷ 2 = 10dm
Jawab : a. L. alas = πr² = 3,14 × 10 × 10
= 314 dm²
b. L. selimut = 2πrt = 2 × 3,14 × 10 × 25
= 1570 dm²
c. L. permukaan = 2πr (r+t) = 2 × 3,14 × 10 (10+25)
= 62,8 × 35 = 2.198 dm²
d. Volume = πr²t = 3,14 × 10 × 10 × 25
= 7850 dm³
Cara mencari garis pelukis yaitu : √t²+r²
Contoh 1 :
Sebuah kerucut dengan jari-jari 7cm, tinggi 24cm dan π 22/7 . Hitunglah
a. L. alas
b. L. selimut
c. L. permukaan
d. Volume
Jawab :
a. L. alas = πr² = 22/7 × 7 × = 154 cm²
b. L. selimut
s = √t²+r² = √24²+7²
L. selimut = πrs = 22/7 × 7 × 25
= 550 cm²
c. L. permukaan = πr² + πrs = 154 +550 = 704 cm²
d. Volume =
Contoh 2 :
Sebuah kerucut dengan garis pelikis 13 cm, tinggi 12cm dan π 3,14. Hitunglah
a. L. alas
b. L. selimut
c. L. permukaan
d. Volume
Jawab :
Sebelum menjawab pertanyaan di atas kita harus mengetahui terlebih dahulu berapa nilai r. Dengan cara √s²-t² = √13²-12² = √169-144 = √25 = 5
Jadi nilai r adalah 5
a. L.alas = πr² = 3,14 × 5 × 5 = 78,5 cm²
b. L.selimut = πrs = 3,14 × 5 × 13 = 204,1 cm²
c. L.permukaan = πr² + πrs = 78,5 + 204,1 = 282,6 cm²
d. Volume =
Itulah BANGUN RUANG SISI LENGKUNG KELAS IX KURIKULUM 2006 BERIKUT CONTOH SOAL DAN GAMBAR semoga bermanfaat :)
ArtikeL terkait :
1. TABUNG
Sebuah tabung memiliki: Jari-jari (r), Tinggi (t) dan Phy (π)Nilai π adalah 22/7 atau 3,14
22/7 hanya digunakan jika bilangan bisa dibagi 7 dan jika 3,14 digunakan jika bilangan tidak bisa dibagi 7
A. JARING-JARING TABUNG

Contoh 1 :
1. Sebuah kaleng berbentuk tabung dengan jari-jari 7cm, tinggi 15cm, dan π 22/7. Hitunglah
a. L. alas
b. L. selimut
c. L. permukaan
d. Volume
Jawab :
a. L. alas = πr² = 22/7 × 7 × 7 = 154 cm²
b. L. selimut = 2πrt = 2 × 22/7 × 7 × 15 = 660 cm²
c. L . permukaan = 2πr² + 2πrt
= (2 × 154) + 660
= 306 + 660 = 968 cm²
d. Volume = L. alas × t
= 154 × 15 = 2310 cm³
Contoh 2 :
2. Sebuah drum dengan diameter 20dm, tinggi 25dm dan π 3,14. Hitunglah
a. L. alas
b. L. selimut
c. L. permukaan
d. Volume
d = 20dm = r = 20 ÷ 2 = 10dm
Jawab : a. L. alas = πr² = 3,14 × 10 × 10
= 314 dm²
b. L. selimut = 2πrt = 2 × 3,14 × 10 × 25
= 1570 dm²
c. L. permukaan = 2πr (r+t) = 2 × 3,14 × 10 (10+25)
= 62,8 × 35 = 2.198 dm²
d. Volume = πr²t = 3,14 × 10 × 10 × 25
= 7850 dm³
2. KERUCUT
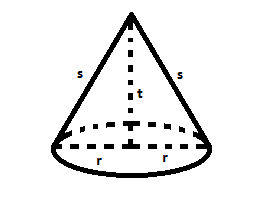
Sebuah kerucut memiliki Jari-jari (r), Tinggi (t) dan Garis pelukis (s)Cara mencari garis pelukis yaitu : √t²+r²
B. JARING-JARING KERUCUT
Contoh 1 :
Sebuah kerucut dengan jari-jari 7cm, tinggi 24cm dan π 22/7 . Hitunglah
a. L. alas
b. L. selimut
c. L. permukaan
d. Volume
Jawab :
a. L. alas = πr² = 22/7 × 7 × = 154 cm²
b. L. selimut
s = √t²+r² = √24²+7²
Baca Juga: loading
= √576+49 =√625 = 25 L. selimut = πrs = 22/7 × 7 × 25
= 550 cm²
d. Volume =
Contoh 2 :
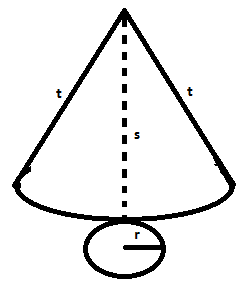
Sebuah kerucut dengan garis pelikis 13 cm, tinggi 12cm dan π 3,14. Hitunglah
a. L. alas
b. L. selimut
c. L. permukaan
d. Volume
Jawab :
Sebelum menjawab pertanyaan di atas kita harus mengetahui terlebih dahulu berapa nilai r. Dengan cara √s²-t² = √13²-12² = √169-144 = √25 = 5
Jadi nilai r adalah 5
a. L.alas = πr² = 3,14 × 5 × 5 = 78,5 cm²
b. L.selimut = πrs = 3,14 × 5 × 13 = 204,1 cm²
c. L.permukaan = πr² + πrs = 78,5 + 204,1 = 282,6 cm²
d. Volume =
3. BOLA
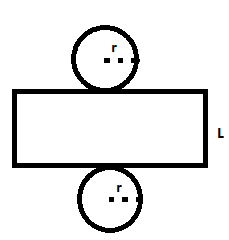
Sebuah bola memiliki Jari-jari (r), dan Diameter (d)
Contoh 1 :
Sebuah bola voly dengan jari-jari 7 dm. Hitunglah
a. L. alas
b. Volume
Jawab :
a. L. alas = 4πr² = 4 × 22/7 × 7 × 7
= 616 dm²
Itulah BANGUN RUANG SISI LENGKUNG KELAS IX KURIKULUM 2006 BERIKUT CONTOH SOAL DAN GAMBAR semoga bermanfaat :)
ArtikeL terkait :



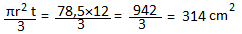



Posting Komentar